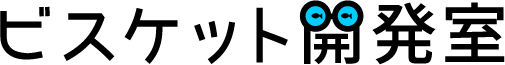では,逆の変換をやってみましょう.
単純に考えると10進法の引き算を作らなければなりません.足し算の場合は2つの数を入れ替えても答えは同じだったので,絵が重なったら足すという約束で作ることができました.引き算は数を入れ替えられないので,今回はマイナスの数をつかって,1を引くという絵をとりあえず作ってみます.


0から−1のとき,9になりますが上の桁に−1を置いているところがミソです.青い三角はクロックで,桁上がりで数がきちんと計算されることが保証するようにしています.
数から順に1を引きながら,それと同期をとって2進法のカウンターで数えれば,最後に0になったときに2進数に変換されています.

三角のクロックが4桁目まで進んだとき,1桁目に戻すと同時に,10進数には−1を2進数には1を足すようにしています.減らしていって

10進数の方が0000になったとき,停止させます.

2進法のカウンタは例によってこのようになってます.
大変実行は遅いですが,一応うごいています.プログラムはここです.
もうちょっとましな方法を考えてみましょう.
まずは,数を薄い青の丸の個数であらわします.

このように0から9までで,青の丸はそれぞれ0個,1個...9個かさなっています.
ここで,パッと見て間違っているかどうかわからないので,テストをしてみます.

重なった丸を2進法で表現してみると,このようになりました.4と,8が間違って一つずつ丸が多いようですね.それで修正してみると,

このように正しくなりました.
このデバッグ用のメガネを削除します.丸の個数で数を表現してますから,数の大小がマッチングで簡単にできます.

最初のメガネは,丸が1つのときはそれを消して2進数の1を生成します.次のメガネは,丸が2つ重なっているときはそれらを消して2進数の10を生成します.3つ目のメガネは,丸が4つ重なっているときはそれらを消して,2進数の100を生成します.
つぎのメガネはとても面白いです.

上のメガネは,丸が8つ重なっていたときは,それを消して2進数の1000を生成します.下のメガネは,10の位に丸が1つあると,それを消して1の位に丸を2つ生成して,2進数の1000を生成します.
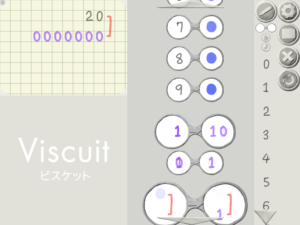
2進法の計算(紫の数字)はこのようにやって,ステージに変換したい10進数の数を黒い数字で表現します.すると,下の紫の数で2進法でひょうげんされたものが出てきます.
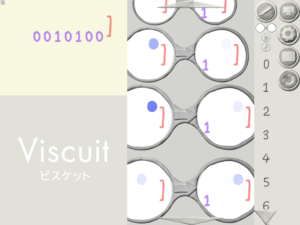
作品はこちらです.
一応5桁目,16ー>10000までは作りました.こちらも同様に丸が1と6ならば100000というのと,10の位が2のき,2進法の10000を生成して,お釣りの4(青い丸が4つ)に変わるものと2つ用意しました.これよりずっと大きな数を変更する場合でも,16を4回引いて64になるといったことが勝手に行われるので,答えを間違うことがないと思うのですが.
とちゅう,フリーズしたかと思わせるくらい計算が遅くなるときがあります.丸が8つ重なったりというメッチングの計算がとても時間がかかります.