これは「言語実装Advent Calendar 2017」の12月6日に向けて書いています.普段の投稿とちがって少し専門家向けに書いています.
最近はプログラミング教育ブームですが,ビスケットはそんなブームになる前からコツコツと作ってきた教育向けビジュアル言語です.一線の研究者から身を引いてからは,あまりビスケットの中身について書くことは無かったのですが,いい機会なのでこのカレンダーに参加しました.
ビスケットは絵を動かすために絵でプログラムを作る言語です.これはたとえば,数値計算のためにFORTRANが生まれたり,知識表現のためにLISPが生まれたり,という背景と同じです.なにかを計算対象とするプログラミング言語はその対象と近い表現形式を取るべきであるということです.
たとえば,絵が動くアニメーションのためには普通の言語でしたら move(10, -50) というように表記しますよね.XとYの座標の差分を指示することで絵の動く方向と速度を指定しています.それをビスケットでは,
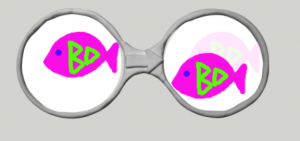
のようにプログラムで表します.この基本要素をメガネと読んでますが,メガネの左側が以前,右側が以後で,変化を表しています.左側にさかなが上の方にあって,右側にさかなは斜め下にあるので,これは斜め下に動くという命令になります.
ビスケットはルール型の書き換え言語ですので,この命令はいつ実行するか,というタイミングはなくて,ステージにこのさかなが置かれれば常にこの動きを続けるということになります.
言語の中身ということで,ビスケットを作る上で何が難しいかということを話します.私がいままさに取り組んでいる問題から.
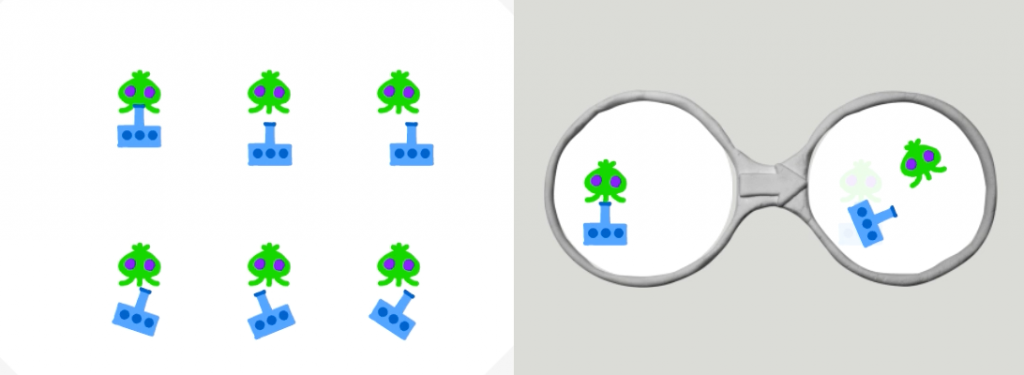
ビスケットではメガネの左側に絵を2つ以上入れると,「その配置が画面上に現れたら」という条件として動きます.同時に右側にも絵を入れることで,それらの絵がどのように一緒に動くかという指示になります.動き終わった後もその配置になれば,何度も移動は繰り返されます.このような絵の配置で条件判定をするプログラミング言語には,1994年くらいの先行研究としてKIDSIMが有名です.KIDSIMは格子状に並んだアイコンの配置を書き換える言語でして,当時のコンピュータパワーからすると画期的な言語だったと思います.
ビスケットはそれに対して,回転できて任意の位置に置けるアイコンを書き換える言語という拡張をしました.このとき,厳密なマッチングではなく大体配置が似ていたら書き換えるということになります.それで上の図ですが,メガネの左側には「宇宙人と砲が縦に並んだ時」となってますが,ステージには6パターンで縦に並んだ状態が置かれています.これらすべてについてメガネの条件が成立して,書き換えが起こります.
書き換えは,メガネの右側の配置にするということですが,それもメガネのまったく同じ配置をするのでは面白くありません.ここは,対象とのずれに応じた変化をさせたいところです.
今のビスケットではこのように変化します.
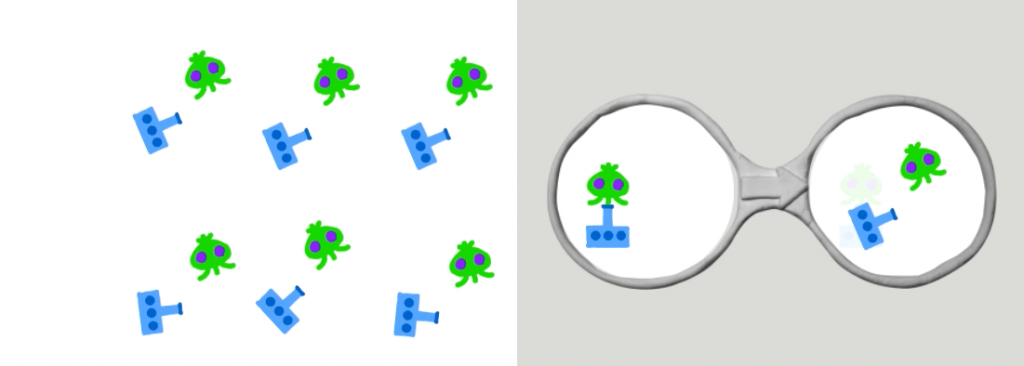
元の配置で,中央上のセットはメガネの左と大体同じような配置です.なので,書き換え結果もメガネの右側と大体同じような配置になります.それ以外は,いろいろとずれているので,そのずれに応じて書き換え結果も変わるようにしています.
メガネが1つの場合は動くか動かないかですが,2つ以上ある場合はどちらのメガネの配置に近いか,という計算をします.つまり,絵の配置同士を比較して一致度を計算しています.
書き換えの各ステップでは,ステージにある絵は1回の書き換えにしか参加できません.それで,すべての絵の組み合わせとメガネの左側とで,絵の配置の一致度を計算して,一番一致した組を書き換えそれらを使用済みにして,未使用の中でさらに一致度が高い組を取り出し,ということを繰り返して,一致度が一定以下になるまで書き換えを繰り返します.
この一致度の計算がなかなか曲者でして.ここで使っている絵は回転に敏感な絵ですが,例えば丸いボールですとか,星の形のような絵は,向きはそれほど気にしません.でもビスケットでは絵の中身はみないので,回転に敏感か鈍感かの区別なしに一致度を計算してしまっています.ですので,ロケットと星がぶつかるプログラムで,星に当たる向きによってぶつかりやすかったりにくかったりするのはこのせいです.これが今の課題その1.
さらにややこしいのが,今のバージョンのビスケットでは禁止していますが,絵のスケールを変える問題があります.前のバージョンでは絵を自由に拡大縮小して置くことができました.メガネの左右でスケールが違えば,書き換えのたびに少しずつ絵が大きくなったり小さくなったりするような効果もありました.ところが,メガネの左側の2つの絵のスケールが違って,書き換え対象の絵のスケールもそれらとも違うという場合,どのように一致度を計算すればよいでしょうか.たとえば,感覚的には星を大きくしたら,ロケットとぶつかりやすくなるはずですが,それがちゃんと計算できているでしょうか.少なくとも前のバージョンでは,子供が無意識に絵の大きさを変えて作ったプログラムで「あれ?うごかないよ」というケースが色々とありまして,そんなこんなで今のバージョンでは絵の大きさを変えられないようにしています.
最初の頃のバージョンではとにかく動くことを優先したので,いろんな計算の妥当性を犠牲にして作ってきました.しかし,時間が経つにつれて,いい計算方法が浮かぶのですね.
今の計算方法は次のようにやっています.
絵を2点で表します.一つは絵の中心,もう一つは絵の真横に一定距離離れた点です.絵が回転したら真横の方向も変わります.また,いまはまだやっていませんが,回転に敏感かどうかは,どれくらい絵の中心から離れるかで調整しようと思います(敏感な絵ほど離れる).
メガネの左側に置かれた絵の各点同士の距離を求めます.絵が2つ置かれていれば,4点あるので,それら同士の距離が6つありますが,そのうち2つは定数なので,4つの距離です.同じように書き換え対象から絵の組を見つけてきて,それらの4点の距離を求めて,それぞれの距離がどれくらい一致しているかを調べます.この計算方法では2つの絵の相対的な位置関係が同じであって(だけど全体として回転している)という状態をうまくマッチングできます.
回転に敏感かどうかも多分うまく行きます.
スケールに対応できるかどうかはまだちょっとよくわかりません.
この計算方法は今のバージョンに採用されています.
もう一つ必要な計算が,どのように書き換えるかです.完全に一致しなかった場合どのような位置関係に書き換えるべきでしょうか?これについては,最近までまったくもってどのような計算をするのが妥当なのか見当もつきませんでした.つまり,今のバージョンの動きはかなりアドホックな計算をしています.
ところが最近とても活気的な計算方法が見つかりまして,いまその更新を頑張っている最中です.完成したらご紹介できると思います.
しかし,このような書き換えエンジンの更新というのは,今まで動いていたプログラムが動かなくなるということでもあるので,古いバージョンも残したりと,なかなか面倒ではあります.
解説というか,誰にもこぼせないような愚痴を書いたようですみません.
しかも,プログラミング言語の理論の人たちが集まるカレンダーでしたね.