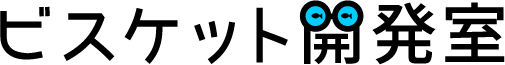よく考えると,これまでメガネの動作についてちゃんと書いたことがなかったですね.例によって,ビスケットの最初のバージョンから少しずつ変わってきているんですが,変わった理由はそれなりに面白いんで書いてみます.
ただし,メガネの動作は結構難しい(と言っても工学部の大学1,2年くらい)数学ですので,極力わかりやすくなるように心がけますけど,それなりに覚悟してお読みください(笑).
ビスケットのそもそもはこれです.
線路と電車の絵を描いて,線路を丸く繋がるように並べて,メガネ1つでその線路の上を走らせる,というものです.なんか,上のブログからのページはうまく動かないみたいなので,こちらのリンクをみてください.
この1つのメガネだけで,たとえば2つの線路が交差したときはちゃんと入り口と出口を間違わないとか,ポイント切り替えみたいなのも作れるとか,そういうのがこのメガネ1つの中に込められていると.
これを思いついたのが,2002年の6月くらいだったと思います.さっそく,どうやって動かしたら良いかわからないけど,まずは構想だけでもと思って,研究会で発表したりしました(これが後で問題となるのですが).
どういう構想かというと,これまでのプログラミング言語は書いたプログラムの通りに動かすだけだったけど,プログラムの意味を拡大解釈しても動くようにできないかということでした.たとえば,
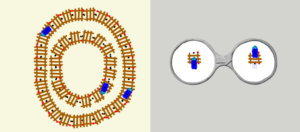
このメガネに対して,下に5つの可能性を作ってみました.左から見ていくと,1番目のは線路と電車の関係はメガネの左側とほぼ同じ,2番目は線路も電車も斜めになっていますが相対的な位置関係は同じですよね.それに対して,3,4,5はちょっとずれています.3番目は少し離れています.4番目は電車が斜め,5番目は線路が斜めですね.相対的な位置関係ということで考えると,4番目と5番目は向きが逆ですが同じ関係にあります.つまり,並びが少しずれているというのは,位置がずれている,角度がずれているの2通りあるということですね.
そういう多少ずれている絵に対しても,メガネがちゃんと動いて欲しいわけです.やって欲しいことを言葉で言うと,電車が線路の反対側に進む,ということですね.
で,1番と2番に関しては,メガネの並びと大体同じなので,結果は次のようになります.

これでもそれなりに面倒な計算が必要なんですよね.sin, cosがごちゃっと出てくる感じです.でもこれは答えがわかっている計算なので,やればいいだけです.問題は次の3つ.
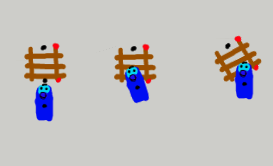
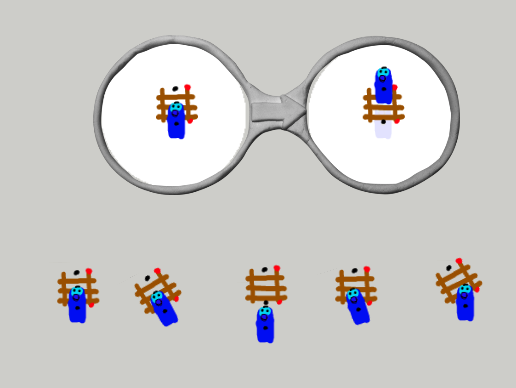
このように,少しずれてステージに絵が並んでいるときに,どのように動けばよいでしょうか.まず,回転がなくて位置がずれている場合は,

このように3通りの可能性があります.左側のは,対象がどれくらいずれているかに関係なく,メガネの右側と同じ結果にするというものです(A).右側のは,対象のずれ(この場合は電車の半分の長さ分下にずれている)がそのまま結果に反映させてます.つまり,メガネの右側と同じ結果から,半分の長さだけ電車を下にします(C).で,真ん中のはその中間です.Aの方法で計算した位置と,Cの方法で計算した位置のちょうど中間になるようにしています.3つともそれぞれ理屈が成立するので,絶対的にどれがよいというのは簡単には決められません.
3つの計算を,ロボットとテニスのラリーをする例えで説明しましょう.できるだけ長く続けるのがゴールです.まずボールを打ちます.ロボットは来たボールを打ち返してくれます.
Aの場合は,ロボットからの返球は必ず真正面に打ち返してくれます.あまり変なところに打ったらロボットは打ち返せませんが,打ち返せた場合はどんな変なコースであっても真正面に打ち返してくれます.これ,ラリーは続きますけど,楽しくないというかやってて辛くなりますよね.
Cは逆に,こちらが真正面からずれたボールを打とうものなら,ロボットは正確に同じだけずらして打ち返してきます.こちらがその打ちにくいボールから体制を立て直して真正面に打ち返せたらよいのですが,多分さっきよりもさらにずれますよね.ロボットはラリーを続けることに非協力的で,意地が悪くこちらのミスをカバーしてません.すぐに破綻しそうです.
で,Bは両方の性質の中間です.こちらが真正面に打てたらちゃんと真正面に打ち返してくれますが,ずれると少しだけ修正して打ち返してくれます.そこそこ楽しくて,破綻もあまり起きない.
と言うような理由により,いまのビスケットはBの計算をします.ただし,これは絵が回転していない場合です.

絵の回転がずれている場合も,同じように3つのケースが考えられますね.左側はメガネの右と同じもの,右側が電車の回転のずれはそのまま結果に反映,真ん中のはその中間.で,ビスケットは中間を選んでいます.
もう少し難しい例をみてみましょう.
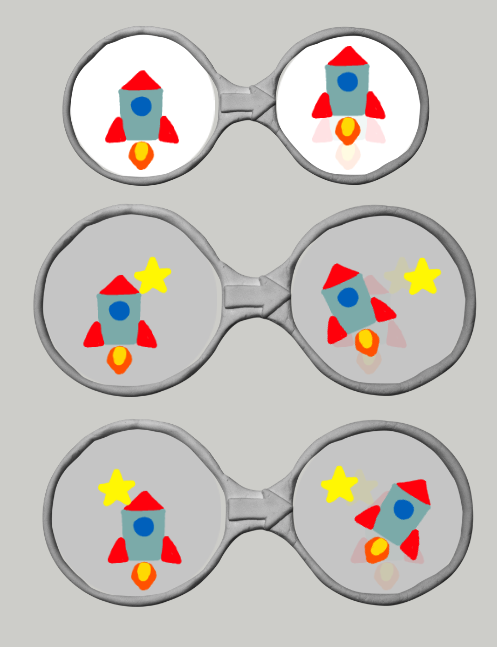
これは,ロケットが何もないところではまっすぐ進む.ロケットが右に星とぶつかると,左に曲がる(星も少し飛ばされます).ロケットが左に星とぶつかると,右に曲がる(星も少し飛ばされます).これがどのように動くのかはそんなに難しくないのですが.これが人間が「思ったように」動くのは結構難しいのです.
まず,星がどれくらい離れているときにぶつかったことにするか.これをきちんと決めないと,「それ以外のときはまっすぐ進む」ができません.電車と線路の場合はメガネが1つだけだったので,できるだけ拡大解釈をして動き続けようとするという姿勢でよかったのですが,メガネが2つ以上あるとどっちのメガネを使うかを決めるので,拡大解釈はほどほどにしなければなりません.

これは,どちらも星とロケットがぶつかってます.元のメガネからすると,右側の方が近い感じがしますよね.でも,これ左側の配置の方がメガネに近いのです.なぜでしょう.というかひっかけ問題でした.
実は,右側の配置では,星は大体180度回転しています.でも,星って回転してもあんまりよくわからない絵ですよね.
わかりやすくするために,星の代わりに土星の絵にしてみました.すると,

実は,こういうことだったのです.これ,ロケットの立場から見ると土星が反対向きになっていると見えますが,土星の立場でみてみると.

のようになります.つまり左側は土星の左下からロケットが当たった場合,右側は土星の右上から下向きのロケットが当たった場合,ということなんです.これだと全然違うでしょ.
でも,星の絵だとその違いに気づくことはほとんどなく,どっちも同じように当たっている感じがします.
それで,最初の頃のビスケットではこの計算はいい加減だったので,当たっているようで当たらなかったり,当たって欲しくない時にも当たっちゃったり.あまり直感的ではない動きをしていました.
要するに,メガネを拡大解釈するときに,人間に自然に見える拡大解釈はなにか,という問題を考えていたのですね.
今のバージョンはどうしているかと言うと,絵の属性として大体の大きさを計算しています.この場合,星は土星よりと結構小さい絵ですよね.で,小さい絵は回転の感度を低く,つまり180度回転したくらいでもぶつかるようにしてます.逆に大きい絵は当たる向きも考えなければならないようになってます.つまり大きな絵に当てるには,いろんな当て方のメガネを増やす必要があるということですね.
で,これが今は絵が2つの場合ですが,絵が3つ以上の場合に拡張しなければなりませんし,いろんなケースごとに動きを考えていては,生合成が取れなくなります.要するに,メガネをほんのちょっと変えた時は結果もほんのちょっとだけ変わってほしいわけですが.計算方法が適当だと,どこかに境界線があって,その境界線をまたぐようにほんのちょっと変えてしまうと結果がガラッと変わってしまう,ということになってしまいます.つまり変化が滑らかになっていなきゃないということです.
なんか,書いてて辛くなってきました.そんなに面白い・感心するような話ではなかったですね.まあ,簡単に思ったように動いてみせるのをプログラムで作るって結構大変なんですよね.
メガネの解釈を機械学習でやったら良いんじゃないかという誘惑もあります.それが正解なのかもしれませんが,一方でちゃんと情報が揃っていれば完璧な計算方法を作れるんじゃないかという期待というか意地もあります.