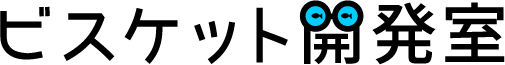昨日ご紹介した2進法でフィボナッチ数列を作り出すプログラムですが,生成される数列は画面の大きさに制限されてしまいます.そこで,画面をスクロールさせて無限に生成させることはできないか考えてみました.
まずは一番基本のメガネ

これをスクロールさせるためにはメガネの右側を1つ左にずらすようにします.つまり,

のようにします.元のメガネは左の^と赤丸が同じ位置にあるのに対して,新しいメガネは^はそのままの位置でその左に青丸,右にも^が生成されます.
同じように丸が重なると上に上がるは


のように斜め上に上がるように.^が重なった場合も


のように斜めに上がります.さらに,今まで静止していた丸も

のように横に動くようにします.これでいちおうスクロールして生成するのがつくれるのですが.



のように,左側に数列がスクロールして生成されてゆきます.
しかし,同じように右のほうにも^が生成されて広がってゆくみたいです.これだとやはり画面のサイズで無限に生成というのは難しいですね.
そこで,^を生成するタイミングを1つずれるようにします.つまり,あたらしく_の絵をかいてこのようにします.
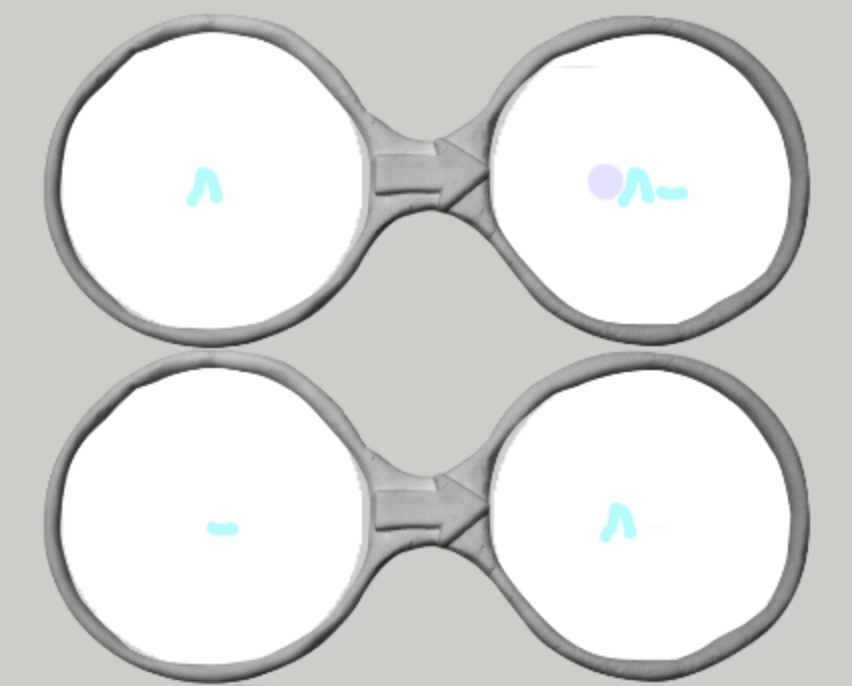
最初は^から丸と^^が生成されるのではなく,丸と^_が生成されます.次に_は^に変わるわけですがそれはスクロールするので左にずれます.
これが生成される列をみてみると,



最初の_が横にずれて^になるのでここで^が2つ重なってます.それで,

_を生成するのをやめて斜め上に^が作られました.

そこからさらに丸と_が作られて行きます.
この生成された列をみてみると,青丸が一度も重なったりしないことがわかります.実は青丸が重なったら斜め上にというメガネは必要なかったことになります.そこで必要なメガネはこの4つです.
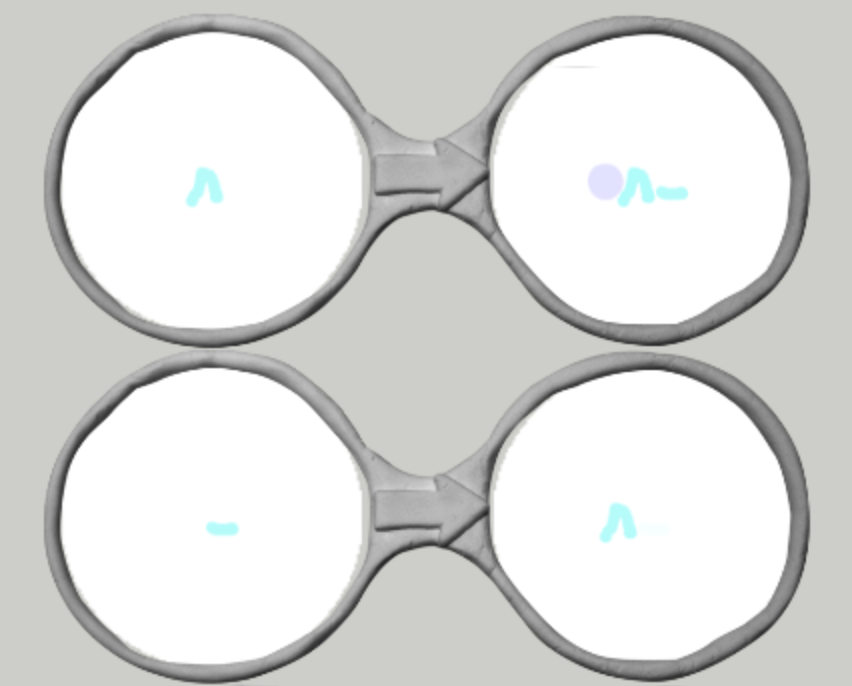
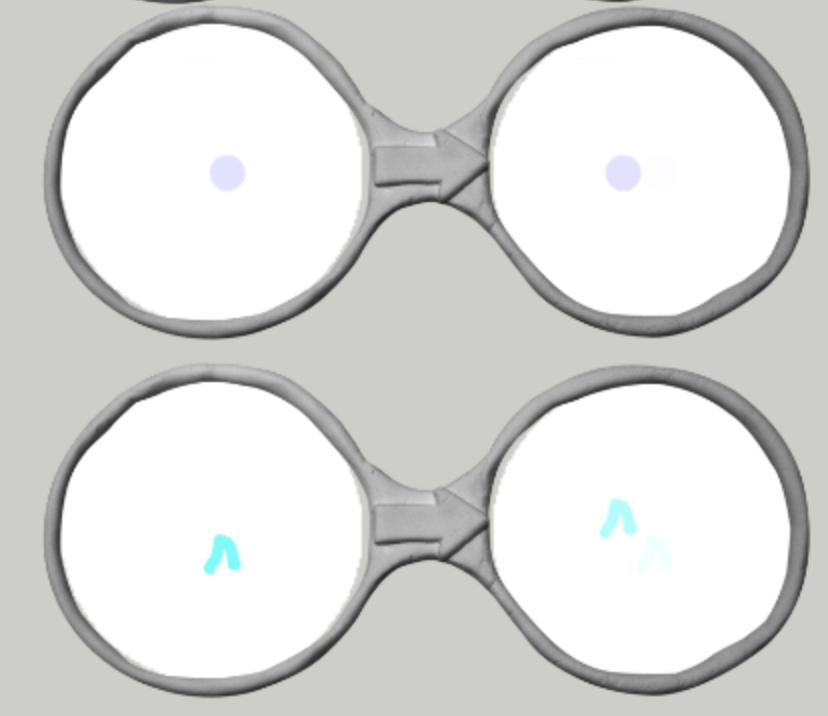
生成される様子は動画でみてみましょう.
画面の縦は24マスあるので,2進法で24桁になります.24桁を超えた分は計算していませんが,この計算は上の桁が下の桁に影響しないので,下24桁だけを取り出したければ,単純に24を超えた分を無視しても問題ありません.
つまり,この先どれだけ計算してもたとえば,1万個目の数は下24桁に限定すればきちんと計算できていることになります.
この列にどういう性質があるでしょうか.ランダムのように見えますが,そんなことはなくて規則性があるはずです.

たとえば,1桁目(一番下)は110が繰り返しているようです.それは当然で,11と並んだらつぎは2になりますからこの桁は0です.01か10はそのまま1が残ります.2桁目は11が6回ごとに現れるようです.1桁目が3回ごとの繰り返しなのでその2倍です.その次が101101が12回ごとに繰り返されてます.どうも,2の倍数の3倍ごとの周期になっているようですね.
これが正しいフィボナッチ数列を計算しているのかどうか,ちょっと自身がないので,他の言語で計算して検算する必要がありそうです.