プログラミングの入門でよく例に出てくるものの一つに「ライフゲーム」があります.2次元のセル・オートマトンですが,そのルールが生命の誕生や淘汰のルールに見えるのが面白いのと,さらにその上で広がるパターンの面白さがさらに奥深いです.
一つのセルには「生きている」「死んでいる」の2つの状態があります.全てのセルが一斉に次の世代に変わるのですがそのとき,生きているセルが次の世代にまで生き残れるのか,それとも死んでしまうのか,死んでいるセルに新たに誕生するのか,それらが周りのセルの生死に影響されるというルールです.
周りのセルは上下左右と斜めでちょうど8つあります.生きているセルの周りに,他に生きているセルが2つか3つあるときは,引き続き次の世代に生き残れます.それより少ないと(0か1つ)過疎で死んでしまい,逆に多いと(4つ以上)過密でこれまた死んでしまいます.逆に死んでいるセルの周りにちょうど3つの生きているセルがある場合,そこに新たに誕生することができます.
ビスケットでは多分作れるだろうという予想はありましたが,八木原さんが初めて作りました.
https://twitter.com/yagi_24bit/status/818093600315621376?s=20
八木原さんのプログラムだと,すこし説明しづらいので,絵を変えて説明しやすくしてみます.
必要な絵は次の5つです.

上から,死んでいるセル,生きているセル,死んでいるセルの計算モード,生きているセルの計算モード,青い丸,です.
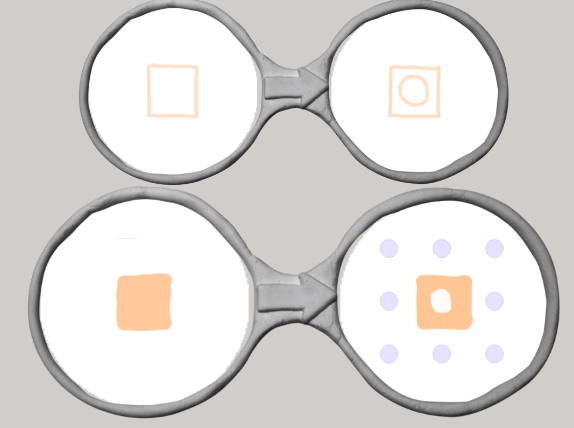
この2つのメガネは計算モードへの移行です.死んでいるセルはそのまま死んでいるセルの計算モードに切り替わります.生きているセルは,自分の周りに青い点を置いて(8つ)計算モードに変わります.
青い点は,周囲のセルからみて,周りに生きているセルがいくつあるかを数えることに使います.
死んでいるセルの計算モードには9つのメガネがあります.
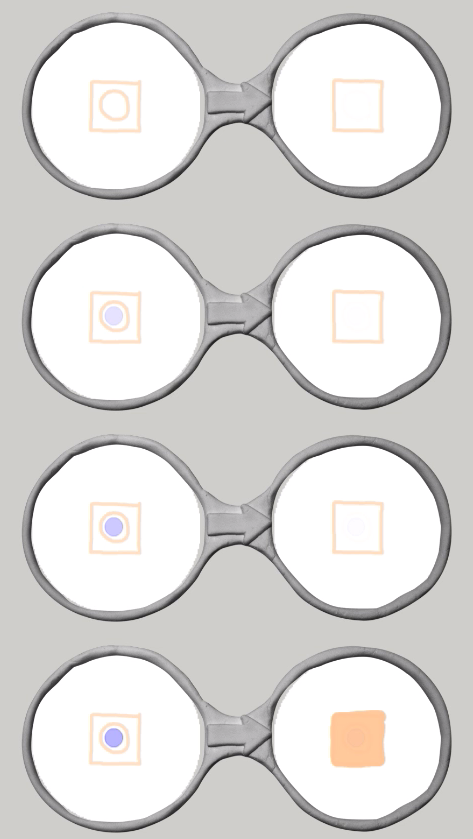
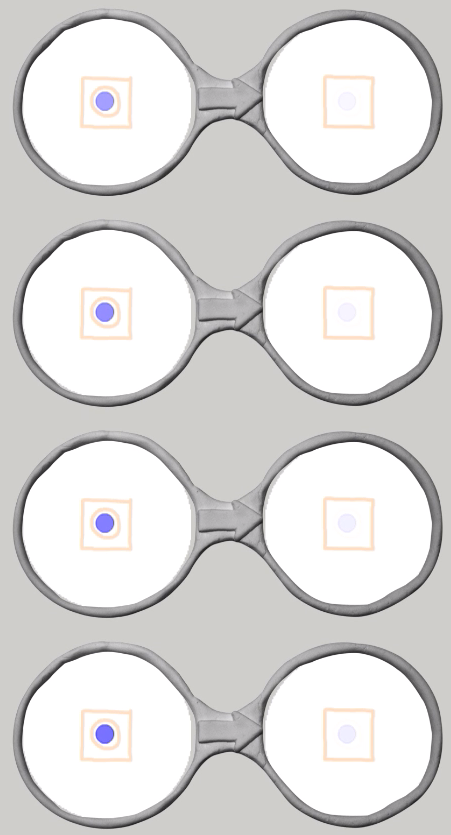

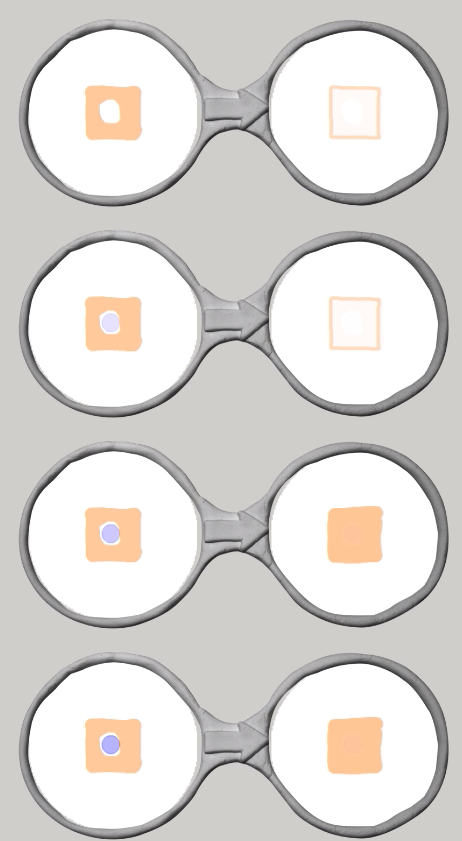
上から順に死んだセルの計算モードの絵に対して青い丸が何個重なっているかで作られています.一番上のメガネは青い丸が0個,つぎのメガネは青い丸が1個,3番目のメガネは青い丸が2個,4番目のメガネは青い丸が3個.最後は青い丸が8個重なっています.9つのメガネのうち,青い丸が3個のときだけ,生きたセルに変わり,それ以外は死んだセルに変わります.ライフゲームのルール通り,死んだセルの周りに生きたセルがちょうど3個あれば,そこに誕生する,というのがそのまま表現されています.
生きたセルの計算モードも同じように9つのメガネでできています.
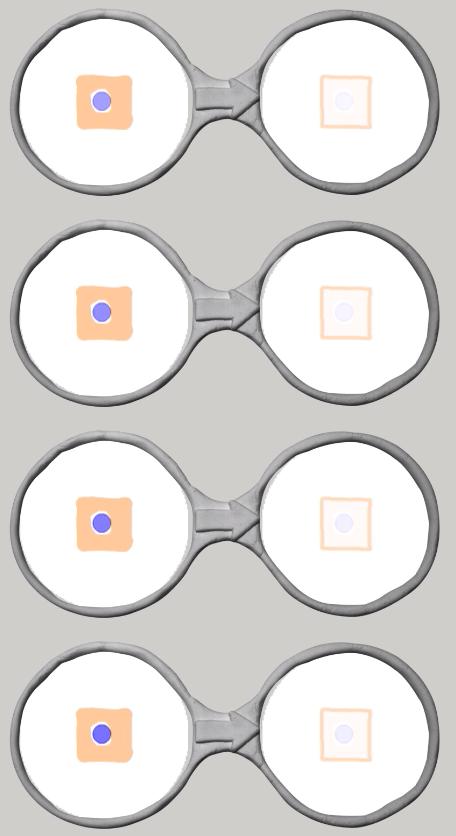

同じように生きたセルの計算モードの絵に対して,青い丸が0個から8個まで,計9個のメガネです.生きたセルが次の世代も生き残るためには,その周りに2つか3つの生きたセルが必要ですが,ここでも青い丸が2つか3つ重なっている時だけ,生きたセルに変わり,その他は死んだセルに変わります.
プログラムはこれで終わりです.実際にどのように動くかみてみましょう.
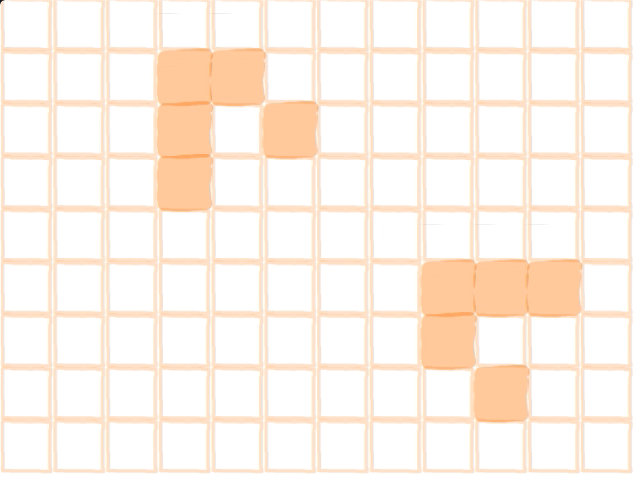
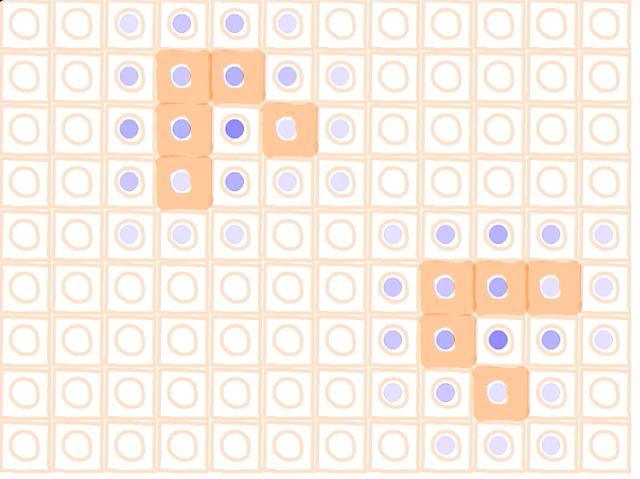
全てのセルが計算モードに一斉に変わります.そのとき,生きているセルの周囲8箇所に青い丸が置かれます.色の濃さで丸がたくさん置かれているということがなんとなくわかりますね.死んだセルで青が3つ重なっているところに新しく発生するわけですがどこかわかりますか?

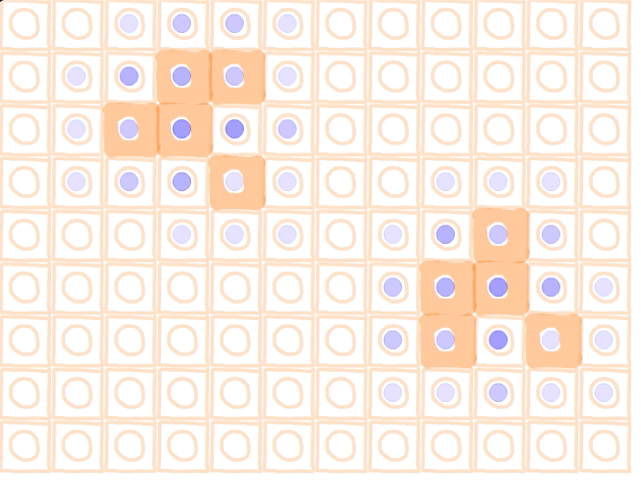

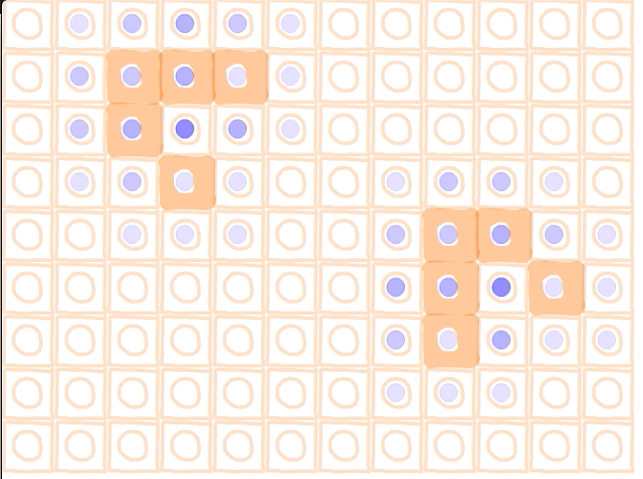

2つのグライダーが飛んでいる様子が見えていると思います.
ビスケットの方眼紙を細かくすればもっと沢山のセルを表現できますが,今のビスケットの作り方がこういうメガネ用にはできていないため,セルが増えるとまったく現実的な速度では動かなくなります.あまり時間がかかると探索の足切りに引っかかってしまうので,計算自体間違えます.グライダー2個くらいしか飛ばせません.そういう速度の問題を除けば,ライフゲームを作ること自体は可能ということでした.
ビスケットでは x > 3 というような数の大小の比較はできないわけですが,全てのパターン0個のとき,1個のとき,… 8個のとき,とメガネに展開すればできてしまいます.
ライフゲームを他の言語で作ろうと思うと,2次元配列を用意して,そこに生きている時は1,死んでいる時は0という数でセルを表して,それぞれのセルに対して周囲に幾つ生きているセルがあるかを数えるプログラムを作って,その数によって次の世代の生死を決めて,それを元にもう一つの2次元配列に次の世代のセルを埋めていって.さらに2次元配列の0と1をグラフィック的に表示するプログラムを作る必要があります.入門用の課題としてはそこそこ難しいですよね.
ライフゲームの本当の面白さはいろんなパターンから初めてどう動くのかを見ることですが,そのためにはセルのパターンを編集するプログラムをつくったりしなければなりません.ところが,ビスケットでは最初のパターンを並べることもビスケット上でできますから新たに作る必要はありません.さらに,何か特定のセルの配置(グライダーなど)を作るメガネを用意すれば,パターンのライブラリー機能があるセルエディタと同じようなこともできます.
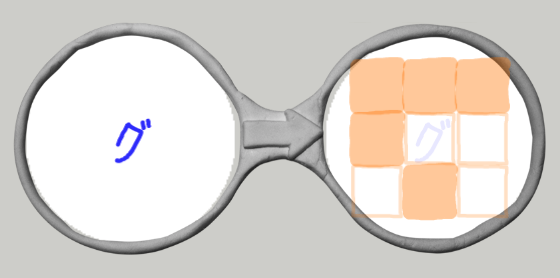
一方で,x > 3 の式で済む部分をメガネで展開しなければならない点ですが,こちらは,次のビスケットで予定されている「メガネの自動生成」の言語拡張のネタになりそうですね.どういう記法でこの生きている時,死んでいる時それぞれの9個のメガネを表すか.面白い課題です.